The  Non-Mathematician's  Guide  To  Basic  Valveless  Pulsejet  Theory © 2008 Larry Cottrill                                                                   by Larry Cottrill   25 Sep 2008 Section 03.03.04 Air Flow Lite Our final "microscopic" example illustrates a couple of additional kinds of actions that a wave can do (although the underlying physical principles are exactly the same, of course). Here we see that we can just as easily have a low pressure wave as a high one, and we also see that expansion doesn't stop when we get to a "normal" air condition. Again we assume (only for the sake of simplicity) that we start out with normal air that is stationary in the pipe. 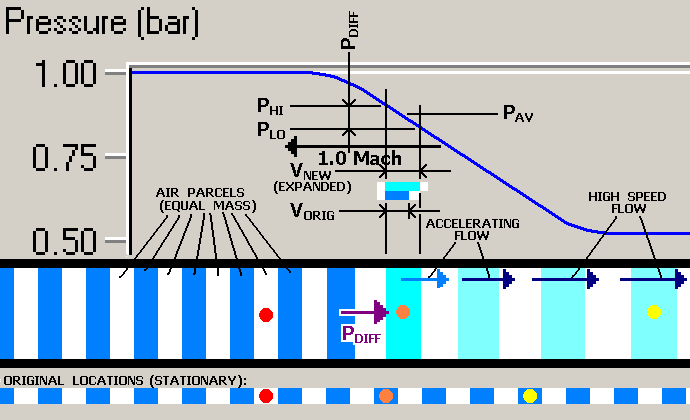A descending wave front that is the leading edge of a low pressure wave advancing (just as before, from right to left): The length of the parcels are now shown at a somewhat smaller scale, in order to clearly show the expansion. Again, the compressibility of air approximately obeys an inverse law -- if we reduce the absolute pressure by half, as shown here, the parcels will expand to almost double their normal volume! The forward speed is also radically increased, as indicated by the displacement shown for the orange- and yellow-dotted parcels. Note that this is really the same action shown for the "trailing edge" of a high pressure wave, shown immediately above -- the PHI pressure acts rightward and the PLO pressure leftward, so the net pressure result is a rightward-acting PDIFF vector (shown acting on the orange-dotted mass). So, there is an acceleration to the right, with a resulting final high speed flow in that direction. The reduced density is indicated by the very light blue of the colored parcels. As you might expect, the temperature of the accelerated parcels has dropped significantly, as well. One important thing illustrated here is that the passage of a low pressure wave has exactly the opposite influence of a high pressure wave on the air mass in the pipe. Such a wave can have just as much air-moving power as a high pressure wave, but always acts to make a change in mass motion in the opposite direction to the traverse direction of the wave. This is true regardless of the direction the wave is moving in the pipe, of course. The "trailing edge" of such a wave would restore the air to its original condition, but displaced some distance opposite to the direction of the wave traverse. Go back to select another Section Next Section:   On Further Reflection ...