The  Non-Mathematician's  Guide  To  Basic  Valveless  Pulsejet  Theory © 2008 Larry Cottrill                                                                   by Larry Cottrill   25 Sep 2008 Section 03.03.05 On Further Reflection ... Now we'll start to look at wave and mass motion behavior at a more "macroscopic" scale. Here is a simplified example of a very common, but quite interesting, phenomenon: the positive reflection of a pressure wave. We will assume a straight pipe vessel with a closed end at the left and an open end at the right. All the contained air starts out stationary in the pipe, and it is all normal air, i.e. the same density and temprature throughout. We induce a pressure pulse in the pipe, traveling from the right toward the closed end at the left. This time, we'll use moderate pressures, more like what we would encounter in a small pulsejet engine. In this illustration, we'll arbitrarily divide time up into 11 approximately equal intervals, from T=0 to T=10. I have clearly indicated the spans of stationary air. The motion of the pressure wave at Mach 1.0 speed is indicated by the long horizontal arrow above the high part of the wave. Again, there would never be a wave pulse with such a "clean" shape in a real pulsejet, but it's perfect for purposes of showing how things happen in this case. As in the earlier drawings, the air in the pipe is divided up into "parcels" of equal mass (this means that before the pressure pulse was applied, they were of equal density and volume -- again, since the pipe is of constant cross-sectional area, they started out with equal length in the pipe). We know from what we just saw that they will be compressed to a lesser length under the high pressure pulse area of the curve, because of the compressibility of air. 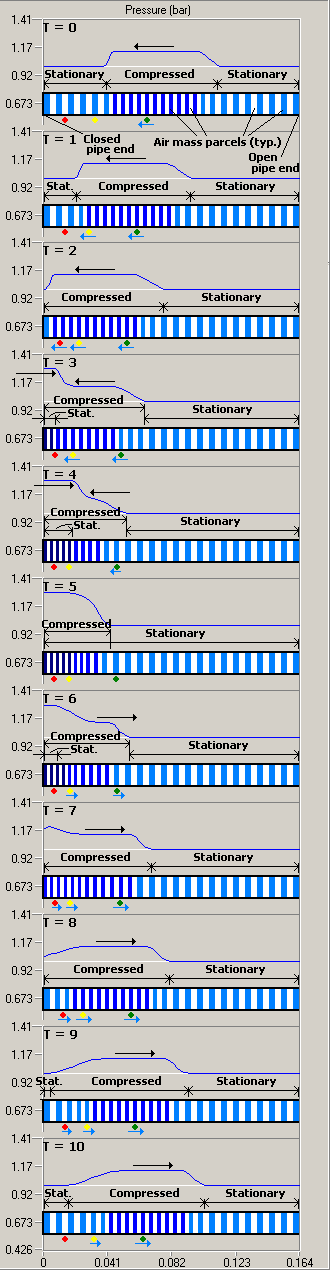At time T=0, the rather long pulse is already in the middle of the pipe, with the uniformly compressed parcels traveling along beneath it. Since the air started out stationary, the compressed parcels are accelerated by the pulse's leading edge and travel in the same direction as the pulse until they are overtaken by the trailing edge, where they are slowed and expanded, becoming stationary once again as they are left behind by the inexorably advancing compressed zone. This can be clearly seen by comparing time T=0 and time T=1, below. At T=2, the pulse just reaches the rigid plate that closes off the pipe end. The air in the compression zone is still moving forward, but now is at the place where it has nowhere left to go! Obviously, the exact conditions under the curve are about to change -- and, in fact, they are going to change radically: A moment later, at T=3, we begin to see some of the magic of flow dynamics: The leading edge of the pulse has been fully reflected by the closed end plate, and the reflected part of the pulse can actually be seen moving at Mach 1.0 from left to right on top of the remnant of the pulse that keeps moving toward the left end! The pressure under this part of the curve is an exact doubling of the "excess" pressure (that is, if the original pulse represented 1.15 bar, the right-moving part of the curve represents 1.30 bar -- .3 bar of "excess" pressure instead of .15). This means, of course, that the air in this part of the pipe is compressed significantly more than it was before, as indicated by the narrowness of the parcels shown in the graph. Also, the parcels beneath this "doubled" area of the curve become practically stationary in the pipe! At T=4, the reflected wave leading edge has almost perfectly covered the flat "plateau" section of the leftward advancing part of the wave. The stationary part of the mass within the wave has now grown so wide that it covers both the red- and yellow-dotted air mass parcels, which are now pretty highly compressed along with those around them. The green-dotted parcel is slowing down and will halt completely when the trailing edge is past. T=5 might as well be called the "midpoint" of the pressure reflection. The right-moving leading edge has "poured down the side" of the left-moving trailing edge, so that part of the doubled wave has the appearance of a smooth, round lump; almost all of the air mass under the curve is fully compressed, but the most astonishing thing to observe is that, just for this brief instant in time, the air velocity in the entire pipe is essentially zero! At T=6, the reflected wave front has clearly broken away from the pile-up, and both the yellow- and green-dotted parcels have been pulled into rightward motion by its influence. Interestingly, the left-moving trailing edge can now be seen at the top of the pressure curve. At T=7, this top part of the curve begins to "melt down" near the closed pipe end. This appearance is totally due to the fact that part of the trailing edge is now reflected and has become right-moving. At this point, even the red-dotted air parcel starts to move right, as the formerly fully compressed air next to the closed end begins expansion. At time T=8, all the air at the left end of the pipe is moving rightward, though the speed near the end plate is very low. All three dotted parcels are following the wave traverse. By T=9, the red and yellow-dotted air parcels are slowing down under the influence of the descending pressure in the trailing edge, which is rapidly passing them by. At T=10, the red-dotted air mass is left behind in a stationary zone, and the motion of the yellow-dotted one is winding down. Only the green-dotted parcel is still in the full-pressure zone of the right-moving reflected wave. One more interesting thing to note: While this appears to be a very "clean" process (in terms of kinetic energy, the rebound of the compressed mass from the end plate is virtually lossless), the reflection is not perfect -- it is not what an audio technician would call "high fidelity". Note how the plateau top of the wave is shortened a little, while both the leading and trailing edges have been "rounded off" and "stretched" significantly. Positive reflections always seem to have some of this "high frequency rolloff" which tries to smooth out regions of sharp pressure change. The reflection behaves something like a "low pass filter", and the change in the shapes of the fronts can be seen as a kind of "distortion". This will have almost no effect on very gradually changing pressures (e.g. long sine curves) but will greatly effect sharp breaks in the pressure curve, especially where the "rise time" is very brief. Since we are usually concerned most with the lowest frequency wave in a pulsejet (i.e. the basic or "fundamental" engine frequency), this isn't usually an important problem. However, in some high-performance engine designs, the relative strengths of the harmonic frequencies (high frequency multiples of the fundamental frequency) can be quite important, and this effect works to degrade them. Go back to select another Section Next Section:   You Gotta Know the Rules