The  Non-Mathematician's  Guide  To  Basic  Valveless  Pulsejet  Theory © 2008 Larry Cottrill                                                                   by Larry Cottrill   25 Sep 2008 Section 03.03.01 A Frontal Assault We know that (by definition) a pressure wave moves through air at precisely 1.0 Mach at the particular temperature and pressure of that air mass. The temperature, pressure and density of the air at a particular location is known as the local air condition. Consider, however, that once the pressure wave has begun to act on the air, the local condition is already changing! For example, once the air lies in a positively pressurized zone, that pressurization has forced the air into higher density, and even raised the air temperature to some extent. This altered condition means that the measured air speed (such as feet/sec or metres/sec) defined as Mach 1 will be higher than in normal air, mostly due to the higher temperature. If we imagine a very simple form for the pressure wave (a plateau of high pressure with sloping leading and trailing edges), the behavior of air under a changing local condition can be easily visualized. Both the leading and trailing edges are called "wave fronts", but we can use just the leading (rising pressure) front as an example; we can assume for now that the trailing (falling pressure) front would show an exactly opposite effect. 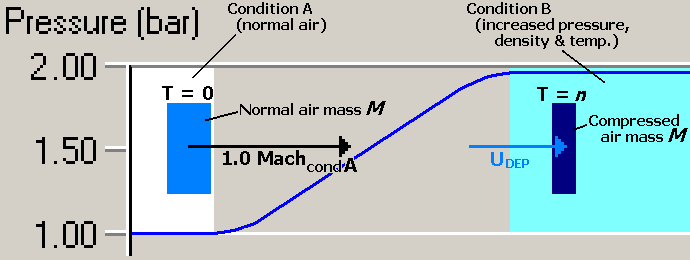Pretend for a moment that we can move along with the advancing pressure wave; we would then view the pressure wave front as "stationary". Pretend also that we can see a small sample of air mass and view what it does over some space of time. At some time we'll again call T=0 suppose we observe a small parcel of air we'll call air mass M approaching us (and the wave front), before it begins to be affected by the increasing pressure. To keep things simple, let's say that the unaffected air out in front of the wave is "normal" air (i.e. standard sea level air pressure at a comfortable temperature) -- we can say that all the approaching air (including the parcel we've chosen to watch) is at the "normal condition", which we'll call Condition A for purposes of comparison later. If we measure the speed of the approaching parcel of air, we quite naturally find it to be equivalent to 1.0 Mach at Condition A (i.e. approximately 321.5 metres/sec for normal air) . Now, as we watch our selected air mass parcel move through the pressure wave front, we can observe changes to its condition. Its mass never changes, of course, but its size (meaning, its volume) does! As the parcel moves through the zone of increasing pressure, its volume is squeezed smaller and smaller; in fact, the volume is changing inversely to the pressure acting on it (that is, doubling the pressure would squeeze it to approximately half its original volume!). So, as we see the parcel travel through the front, we see it gradually shrink. Since the mass remains constant, this means the density of the parcel is gradually increasing. If we observe carefully, we will note one other interesting phenomenon: the speed of the parcel is gradually decreasing! After moving completely through the pressure front (at some later time T=n), our selected air mass parcel has arrived at some new temperature, density and pressure (in other words, a new "local condition" we'll call Condition B), but it ALSO has a new, much lower, speed. What has happened is that some of the wave energy has been applied to the mass, changing both the heat contained in the mass parcel AND its speed. I've attempted to show all this in the graphic below. The bold right-pointing arrows are called vectors; they obviously show direction of motion, but in addition, their lengths are set to illustrate the measurable speeds. Similarly, the width of the parcel at the two locations shows the volume change, and the color is intended to roughly communicate the change in density. The "departure speed" of the parcel behind the wave is designated by the vector UDEP: Now, we might feel justified in re-stating our observation as a simple rule: Assuming a pressure wave front which changes the air condition, the advancing front will see air approaching at a speed of 1.0 Mach under the original condition and will see air departing from it in the original direction but at a significantly lower speed, with the change in mass temperature and the difference in approach and departure speeds representing the total kinetic energy applied to this mass in the passage of the wave front. It is crucial to understand the preceding assertion. From it, the entire theoretical basis for the physical action of the pressure wave on the air mass can be derived. From the standpoint of pure physics, this model already shows an important principle related to changing the velocity of masses: the slowing of the mass as its density increases is actually a demonstration of the conversion of external kinetic energy (the energy of motion) into internal kinetic energy (gas pressure and temperature). This kind of conversion and its reverse are absolutely fundamental to virtually all jet engine dynamics. To help illustrate the effect of the pressure wave on the air condition and departure speed UDEP, I offer the following table. The departure speed could also be given as a Mach number at the local air condition, which I've shown as MachDEP. Note that valveless pulsejets are low compression engines, and a pressure of 2.0 bar will cover all internal pressures normally encountered in design: Departure Speed vs Condition B Pressure   (Condition A = 1.0 bar air at 300 °K) PressCondB TempCondB 1.0 MachCondB UDEP MachDEP 1.1 bar 308 °K 325.2 m/sec 297.9 m/sec .916 Mach 1.2 bar 316 °K 328.5 m/sec 275.9 m/sec .840 Mach 1.3 bar 323 °K 331.6 m/sec 254.7 m/sec .768 Mach 1.4 bar 330 °K 334.3 m/sec 236.7 m/sec .708 Mach 1.5 bar 337 °K 336.9 m/sec 218.3 m/sec .648 Mach 1.6 bar 343 °K 339.7 m/sec 202.1 m/sec .595 Mach 1.7 bar 349 °K 342.4 m/sec 185.6 m/sec .542 Mach 1.8 bar 355 °K 345.3 m/sec 169.2 m/sec .490 Mach 1.9 bar 360 °K 347.0 m/sec 155.8 m/sec .449 Mach 2.0 bar 366 °K 350.0 m/sec 140.7 m/sec .402 Mach The kind of pressure wave shown in this graphic, a "ramp" of increasing pressure leading up to a "plateau" of constant high pressure, is not something we will ever see in a pulsejet, and was chosen basically because it simplifies the illustration of wave front action. This does not mean that there can't be a "real life" wave like this, though -- it actually is a fairly good representation of the pressure wave that moves out in front of a piston moving in a cylinder. Another example would be the pressurization of air in a gun barrel in front of a moving bullet. Go back to select another Section Next Section:   Putting On the Pressure