The  Non-Mathematician's  Guide  To  Basic  Valveless  Pulsejet  Theory © 2008 Larry Cottrill                                                                   by Larry Cottrill   25 Sep 2008 Subtopic 03.02 Kadenacy "Hangs Ten" Like any Big Kahuna on Maui, the Kadenacy action "rides the wave" -- but in this case, the wave is a region of pressure that moves through the air, exactly like a "sound" or "acoustic" wave traveling from a loudspeaker to your ear. This moving region of pressure is, in fact, the only propelling force for the air that is pumped in and out of the vessel. Unlike the magnificent Hawaiian surf, these waves are totally massless, and move through the air in the vessel at Mach 1.0 speed (the speed of sound at the air temperature the wave encounters). Note, however, that this does NOT mean that the air itself is moved at this kind of speed! In fact, actual air mass motion is MUCH slower than the wave motion. Because of this "discrepancy", some people conclude that the wave motion and mass motion are totally unrelated -- but, nothing could be further from the truth! We might tend to think that in our flashlight-shaped pumping vessel, the air in the entire vessel changes pressure together (as it seems to do when we're inflating a balloon). But in fact, we can unequivocally state that it is impossible for air to behave in this way. 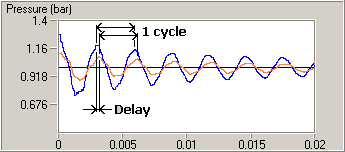We can find a clue to this by looking at our .02 second graph again, but this time superimposing a graph of the pressure as it changes at a point some distance into the long pipe (shown as the orange curve below): The important thing to notice here is that the orange curve is "right shifted" in relation to the blue curve -- meaning that the peaks and valleys of pressure in the pipe are slightly delayed in time from their corresponding highs and lows in the chamber. This suggests that the high and low pressure regions travel through the vessel at some high, but measurable, speed. We can also observe that the amplitude of the pressure swings is much lower at this point than they are at the front of the chamber (the blue curve). Their "shape" is also somewhat different (by that, I mean that the orange curve is not just a "scaled down" model of the blue curve). In fact, I have manually "smoothed" the orange curve somewhat to make the rightward shift easier to see (more about that later), but I haven't tried to intentionally "warp" it in any way just to make it fit. 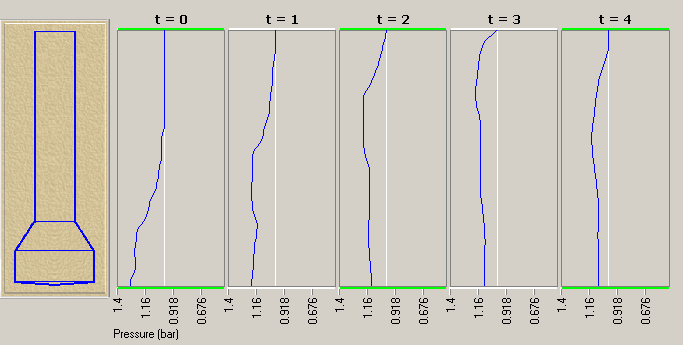Fortunately, just as it is possible to graph pressure against time for a given point in the vessel (as shown above), we can graph how pressure changes throughout the entire vessel at varying points in time. Here is a sequence of time frames showing how pressure regions move through the vessel. In the drawing, I found it more convenient to orient the vessel vertical, with the time frames spread out from left to right as time passes. Just keep in mind that each curve represents the front of the chamber at the bottom and the open end of the pipe at the top. The vertical white line represents normal outdoor air pressure, defined as 1.0 bar. Values to the left of the white line are higher than normal pressures; values to the right are lower pressures. (Note: the frames were arbitrarily selected to illustrate the principle, so the time intervals between frames should not be taken as uniform or "regular" intervals.) We typically start out (at time t=0) with high pressure concentrated in the chamber. This high pressure region moves ("traverses") the vessel rapidly (at the speed of sound) from the chamber to the rear opening, where the excess pressure seems to suddenly disappear! (at time t=4): What actually happens at t=4 is that the energy represented by the positive pressure wave has been transferred to the air just outside the open end of the pipe. This pressure energy immediately creates a spherical acoustic wave radiating outward from a point about 1/3 of the pipe diameter beyond the open end of the pipe (this point can be called the pipe's pressure node). If the power of this radiating wave is low, it is a tiny component of what we perceive as a musical tone; if the power is very high, we hear it as an explosive "bang" - for example, a tiny component of the roar of a pulsejet! What happens next is extremely interesting: The action of the wave energy being dissipated beyond the end of the pipe creates an immediate pressure drop in the open end of the pipe, and this low pressure now becomes a wave that starts to traverse the vessel in the opposite direction, from rear to front! 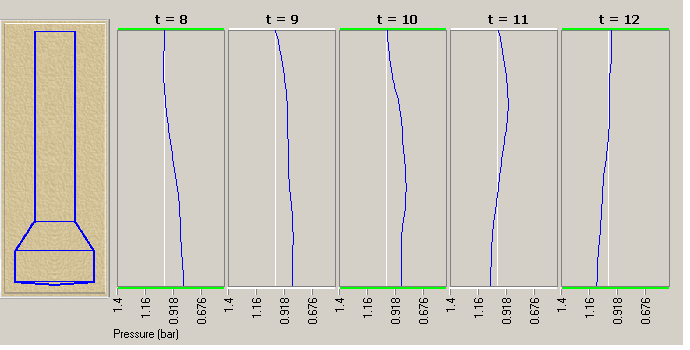This is often referred to as the negative reflection of the pressure wave by the open end of the pipe (we'll start where we left off, at t=4): Note how, as the low pressure wave traverses the vessel, it in effect "pulls" the pressure lower all along its route -- by the time we get to time t=7, the entire pipe has been pulled to less than atmospheric pressure! At t=8, the low pressure has been concentrated in the chamber part of the vessel, in essence a "mirror image" of the conditions at time t=0! (Note, however, that the magnitude of the pressure curve is smaller, due to losses encountered in the process.) This is where we are at the exact halfway point in the acoustic cycle. Unlike a wave arriving at an open end, the energy now represented by pressure at the chamber front end has no place to go but back where it came from. This is the point in the vessel where the highest magnitude pressure swings will occur and is called the pressure antinode. Because there is no dissipation of energy at this point, the low pressure wave propagates back through the vessel -- this is often called the positive reflection of the pressure wave by the closed end of a vessel. The traverse of the wave resembles the earlier traverse of the high pressure wave, but in reduced magnitude and "mirror image" form (starting where we left off at t=8): A careful comparison of the low pressure and high pressure phases of the cycle will show that the action is not absolutely identical. Note especially that in the low pressure phase, the pressure in the chamber actually swings positive even before the low part of the wave reaches the open end of the chamber. (This is because air has actually been moved forward in the vessel by this point in time -- evidence of the "pumping action" of the vessel.) However, the physical principles are exactly the same for the low pressure wave; it will undergo "negative reflection" from the open end of the pipe in the final part of the cycle. So, by the time the cycle is complete (time t=16), the pressure layout in the vessel is restored in a pattern remarkably similar to the starting condition (time t=0): From this point, the entire cycle is ready to repeat -- that is, time t=16 actually becomes time t=0 for the next cycle! So, what we have seen is the creation of a concentrated low-pressure zone, from nothing but the natural physical process begun by initially setting up a high-pressure zone and allowing this pressure to be relieved by somewhat restricted flow to the outside of the vessel; then, we've seen how this automatically results in partial restoration of the original pressure in the very same zone of the vessel. This automatic cycle of pressure variation is precisely what we mean when we talk about "Kadenacy action" or the "Kadenacy effect". The movement of air out of and into the vessel to accomplish these pressure changes is sometimes referred to as "Kadenacy breathing". Every different shape of acoustic device will have a different form of these pressure curves; yet, the underlying principle of "Kadenacy breathing" is exactly the same as we see here. The overall volume and length of the device (and the local density of the air) determine the basic duration of this alternating high and low pressure cycle, and thus the operating frequency of the device. In our graphic examples, there are about 6.75 cycles in the .02 second sampling time, so the cycle duration is: T  =  0.02 / 6.75  =  0.00296 second And the frequency is 1.0 divided by this duration: f  =  1.0 / T  =  1.0 / 0.00296  =  337.5 cycles/sec  (or, 337.5 Hz) (This frequency lies clearly within the audible range of humans, and is about the frequency of some small pulsejet engines.) The exact shape of the pressure wave as it transitions into the air at the open end determines what we perceive as the "voice" or tonality of the sound (and that wave shape is determined by the precise shaping of the acoustic vessel). Thus, we can distinguish the tones of an oboe from those of a clarinet, even if we hear them play the very same sequence of notes. There are only two fundamental physical differences between a musical wind instrument and a valveless pulsejet engine: The pressure swings in the pulsejet are fairly large, as shown in the graphic examples (in a musical instrument, the pressure swings are tiny); and, the interior of most of the engine maintains an extremely high air temperature throughout the cycle (in an instrument, the temperature is essentially the same as the outside air). The main functional difference is that in the jet we need to move significant air mass to realize power development (vastly greater pumping action than in even a huge organ pipe). So far, all we've looked at is pressure -- but that is just the driving force behind mass motion. In the next subtopic, we'll try to see how pressure really works to make air move. Next subtopic:   Power To the Masses! Go back to select another subtopic